Introducción
Nuestra experiencia cotidiana nos llevaría a calificar como absurda la idea objetos constituidos por instancias arbitrariamente similares de sí mismos o, más específicamente, recursivamente construidos mediante objetos de la misma clase. Aceptar esta posibilidad implicaría aceptar como válidas construcciones tan extrañas como una Mesa compuesta de (Mesa compuesta de (Mesa compuesta de (Mesa …))).
Sin embargo, los lenguajes orientados a objetos admiten esta posibilidad que, de hecho, resulta muy útil en escenarios diversos: el Patrón Singleton define una clase que contiene una instancia de sí misma accesible por el resto del programa; el paradigma Entidad-Componente, en sus vertientes más monistas -aquellas donde existe una única clase que simula objetos complejos mediante composición- hace uso de esta recursividad estructural o pseudo-fractalidad inevitablemente. Estructuras de datos muy utilizadas tales como Linked List o Binary Tree también se construyen de forma recursiva por lo que resulta evidente la importancia de conocer esta técnica de programación.
La utilización de este tipo de estructuras puede facilitar la gestión de memoria mediante Pooling de objetos dado que, al existir un único tipo de entidad, podemos reciclarlas y reutilizarlas bajo demanda. No obstante, aunque existen escenarios donde puede resultar interesante el uso de estructuras recursivas -tanto desde el punto de vista estructural como de gestión de memoria- su implementación implica, a su vez, el uso de funciones recursivas para acceder a las entidades anidadas unas dentro de otras, incrementando notablemente la complejidad del código y dificultando su mantenimiento.
Con el fin de aclarar las ideas centrales de la Programación Recursiva y la Fractalidad en lenguajes orientados a objetos -leer anexo sobre Fractalidad al final del artículo-, el presente artículo detalla distintos casos de uso con implementaciones sencillas que pueden servir como punto de entrada para quienes no se hayan enfrentado todavía a la inevitable recursividad de algunos problemas. En mi repositorio se encuentra el código completo utilizado en el artículo programado en C#.
Pseudo-Fractalidad y Recursividad
‘To understand recursion, you must first understand recursion’
Recursion Explained
El concepto de Recursividad nos permite definir métodos que se llaman a sí mismos. Esta funcionalidad permite resolver algunos problemas de forma muy sencilla, existiendo un gran número de situaciones donde la recursión reduce la extensión del código. Un conocido ejemplo de método recursivo podría ser la implementación de una función para calcular el factorial[1] de un número natural:
public static long Factorial(int num)
{
//Caso base.
//Debemos definir un punto de parada para evitar un Stack Overflow.
if (num == 0)
{
return 1;
}
//La función se llama recursivamente a sí misma
//La siguiente llamada utiliza num-1
return num * Factorial(num - 1);
}
Como vemos en el ejemplo, la función long Factorial(int num) se llama a sí misma en la sentencia return num * Factorial(num – 1); las llamadas sucesivas invocan el método restando una unidad a la llamada anterior hasta llegar a 0. Es importante que los métodos recursivos tengan un caso base que corte la recursividad, evitando bucles infinitos que dan lugar a un Stack Overflow. Para ilustrar este primer ejemplo, imaginemos el caso de calcular el factorial de 3; en este caso el flujo sería el siguiente:
//En cada return haremos una llamada recursiva num * Factorial(num - 1);
Factorial(3) -> 3*Factorial(2)
Factorial(2) -> 2*Factorial(1)
Factorial(1) -> 1*Factorial(0)
Factorial(0) -> 1;
//Al llegar al caso base, el programa devuelve en orden inverso las llamadas del return al caso anterior:
Factorial(0) -> 1
Factorial(1) -> 1*Factorial(0) -> 1
Factorial(2) -> 2*Factorial(1) -> 2*1*Factorial(0) -> 2*1
Factorial(3) -> 3*Factorial(2) -> 3*2*Factorial(1) -> 3*2*1*Factorial(0) -> 3*2*1
//Por tanto
Factorial(3) -> 3*2*1
Tal y como mencioné, la recursividad puede reducir la extensión del código en algunos casos. Si utilizamos el operador ternario, podemos escribir el método de cálculo del factorial en una sola línea:
public static long FactorialOneLine(int num)
{
return (num == 1 || num == 0) ? 1 : num * FactorialOneLine(num - 1);
}
Otro caso muy conocido para ilustrar la Recursividad es el del cálculo del término n-ésimo de la Sucesión de Fibonacci [2]:
static void Main(string[] args)
{
for (int i = 0; i < 10; i++)
{
Console.WriteLine(Fibonacci(i));
}
//Resultado: 0,1,1,2,3,5,8,13,21,34
}
public static int Fibonacci(int n)
{
//Casos base
if (n == 0)
return n;
if (n == 1)
return n;
//La función se llama recursivamente a sí misma
return (Fibonacci(n - 1) + Fibonacci(n - 2));
}
En este segundo ejemplo, la función se llama recursivamente dos veces en cada iteración en la que la ejecución llega a la sentencia return (Fibonacci(n – 1) + Fibonacci(n – 2)). De nuevo, con el operador ternario podemos escribir todo el método recursivo en una única línea:
public static int FibonacciOneLine(int n)
{
return (n == 1 || n == 0) ? n : (FibonacciOneLine(n - 1) + FibonacciOneLine(n - 2));
}
Supongamos ahora que queremos abordar el problema planteado en la introducción. Por simplicidad, vamos a crear un objeto recursivamente compuesto que contiene un atributo donde almacena un número natural (num) y una referencia a su mismo tipo para simular la fractalidad (inner):
public class PseudoFractal
{
//Propiedades
public int num { get; set; }
//El objecto incluye una referencia a una instancia de su misma clase
public PseudoFractal inner { get; set; }
//...
}
Tal y como se puede comprobar, la clase descrita en el código puede contener a su vez una referencia a una clase interna PseudoFractal que, a su vez, puede contener otra referencia a otra instancia PseudoFractal; y así sucesivamente. Para construir estos objetos compuestos conviene definir una clase auxiliar que haga las veces de Factory y se encargue del proceso de instanciación recursiva:
public class FractalFactory
{
//Función pública para recibir request
public PseudoFractal BuildToOrder(int order)
{
return RecursiveBuild(order, new PseudoFractal());
}
//Función recursiva para construir objetos pseudofractales a profundidad n.
private PseudoFractal RecursiveBuild(int n, PseudoFractal instance)
{
if (n == 1)
{
return instance;
}
else
{
//Creamos un objeto en cada iteración
PseudoFractal iteration = new PseudoFractal();
//Llamada recursiva.
//Asociamos recursivamente cada objeto al de la iteración anterior
//El resultado es un conjunto de objetos con referencias al siguiente
//Se puede imaginar como anidados uno dentro del otro.
instance.inner = RecursiveBuild(n - 1, iteration);
}
return instance;
}
}
En este caso, hemos separado la lógica recursiva de la gestión de request en dos métodos. El comportamiento recursivo se da en PseudoFractal RecursiveBuild(int n, PseudoFractal instance). De nuevo, tenemos un caso base que corta las iteraciones cuando n llega a 1. En cada llamada, se le asigna al objeto el producto de la siguiente iteración: instance.inner = RecursiveBuild(n – 1, iteration). De esta manera se consigue una estructura de objetos anidados que simula un comportamiento fractal al mantener cada uno de ellos una referencia al siguiente. Este comportamiento simulado sólo es pseudo-fractal desde el punto de vista lógico ya que en memoria cada objeto está instanciado por separado y el vínculo entre los mismos sólo existe como referencia al siguiente.
Para comprobar que todo funciona correctamente, podemos añadir un método adicional a la clase PseudoFractal que acceda recursivamente a sus clases internas y nos proporcione la suma de toda la estructura de objetos anidados. La clase definitiva quedaría en la forma:
public class PseudoFractal
{
//Propiedades
public int num { get; set; }
//El objecto incluye una referencia a una instancia de su misma clase
public PseudoFractal inner { get; set; }
//Constructor
public PseudoFractal()
{
num = 1;
//Por defecto, el objeto no contiene instancias internas.
inner = null;
}
//Método para calcular la suma de toda la estructura recursiva.
public int TotalSum(int res, PseudoFractal instance)
{
//Caso base
//Si es null, la instancia ya no contiene más instancias
if (instance.inner == null)
{
return res += instance.num;
}
else
{
//Sumamos el num de la instancia
res += instance.num;
//Pasamos la instancia interna a la próxima llamada recursiva
PseudoFractal iteration = instance.inner;
return TotalSum(res, iteration);
}
}
}
Finalmente, en el método main instanciamos la clase FractalFactory y la utilizamos para comprobar si genera la estructura esperada. Como ejemplo, tratamos de construir un objeto con tres niveles de profundidad:
static void Main(string[] args)
{
FractalFactory factory = new FractalFactory();
PseudoFractal composite = factory.BuildToOrder(3);
Console.WriteLine($"Total Sum: {composite.TotalSum(0, composite)}");
Console.ReadLine();
}
Al ejecutar el programa, verificamos que la estructura obtenida era la que esperábamos. La función TotalSum devuelve el valor 3 dado que tenemos tres objetos anidados, cada uno con un valor num = 1.
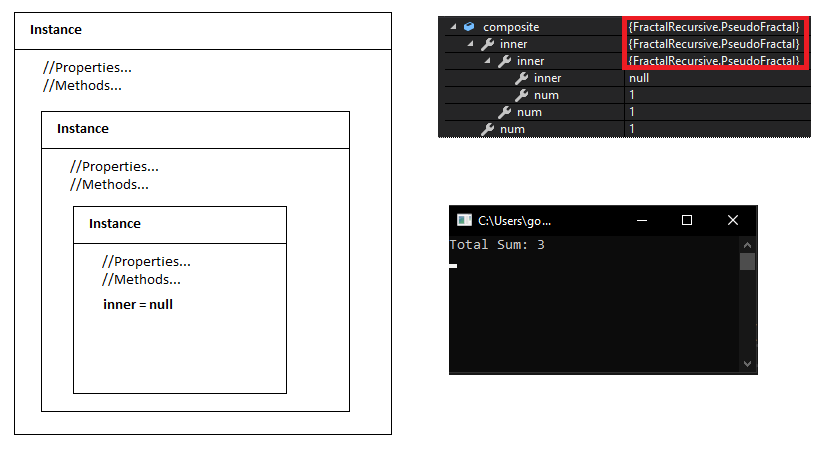
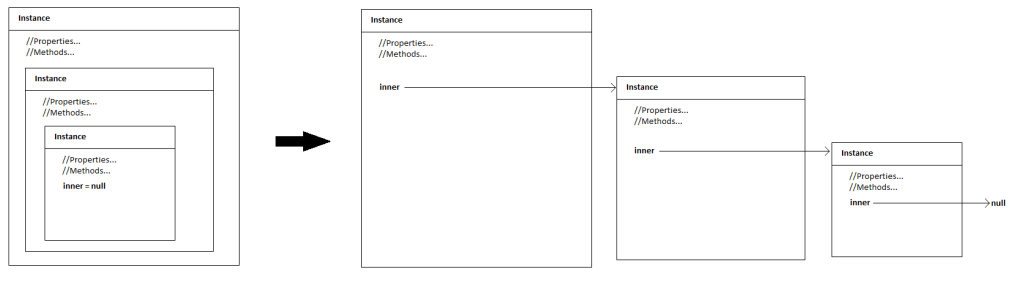
Habiendo conseguido el resultado que buscábamos, cabe volver a realizar un comentario respecto a la estructura de estos objetos en memoria. Los objetos recursivamente compuestos o pseudo-fractales no están estrictamente anidados uno dentro de otro; cada instancia guarda una referencia en memoria al siguiente objeto, pero cada uno de ellos está almacenado en memoria por separado. Es decir, esta familia de objetos sólo es pseudo-fractal en cuanto a su definición lógica y las referencias que mantiene cada objeto respecto del siguiente; sin embargo, en memoria están instanciados independientemente como si fueran objetos separados. Por tanto, hay que enfatizar que la pseudo-fractalidad aquí implementada sólo existe desde un punto de vista lógico y conceptual, no desde la instanciación física de estos objetos en memoria.
Anexo sobre Fractalidad
El término Fractalidad no es del todo coincidente con la definición rigurosa de Fractalidad en el campo de las matemáticas dado que trabajamos con una estructura lógica, no topológica; y por tanto no podemos hablar de aspectos geométricos o de dimensionalidad fractal. En un sentido más estricto, se podría decir que es autosemejante o autosimilar. Por otro lado, al contener referencias a su propio tipo, también se podría defender que es autorreferencial. En cualquier caso, en la bibliografía [4] se suele usar el término Fractalidad en un sentido más laxo para hacer referencia a estructuras que presentan este tipo de comportamientos:
Fractal programming is a programming paradigm based on the concept of “elastic objects”, which can transformed (unfolded and folded) dynamically at run time using strategy planning model and production rules. These rules are keeping the object structure self-similar, thus it has fractal property: parts similar to the whole. The paradigm aims to optimize searching of suitable workflow structure of the object at run time. The elastic object models, production rules integrated by iterated algebraic system, and adjustment strategy planning model are introduced.
Alexander S. Semenov. Essentials of Fractal Programming
Referencias
[1]Recursión para el factorial de un número
[2]Recursión para términos de la Serie de Fibonacci
[4]Essentials of Fractal Programming – Alexander S. Semenov
Enlaces de interés
- Recursion – Good, Bad, or Indifferent?
- Is recursion good or bad in programming – Discusión sobre rendimiento, mantenimiento y elegancia en código en comparación con bucles tradicionales.